2.7.2 Spektralversuch II

1.		2.
	Wasserstoff-Lampe		Spektrum der Wasserstofflampe

1. Bild:	Das Foto zeigt eine Wasserstofflampe. In dieser werden Wasserstoffmoleküle durch einen Elektronenstrahl in angeregte Wasserstoffatome zerlegt, die dann ihre Anregungsenergie in Form von elektromagnetischer Strahlung abgeben. Ein Teil dieser elektromagnetischen Strahlung liegt im sichtbaren Bereich des Lichts.
2. Bild:	Die Wasserstofflampe liefert, im Gegensatz zu der in 2.7.1 gezeigte Wolframlampe, kein kontinuierliches Spektrum, sondern diskrete Linien. Vier dieser Linien befinden sich im sichtbaren Bereich des Spektrums, der Rest liegt im ultravioletten und im infraroten Bereich. Von den 4 sichtbaren Linien erscheint die rote am hellsten, weshalb die Wasserstofflampe auch rot erscheint.

Das hier gezeigte Spektrum ist Teil der sog. Balmer-Serie, deren Gesetzmäszlig;igkeit gegen Ende des 19. Jahrhunderts von dem schweizerischen Lehrer Johann Jakob Balmer durch Ausprobieren gefunden wurde. Der allgemeine Zusammenhang, nach dem sich alle Linien des Wasserstoffspektrums aufbauen, wurde von dem schwedischen Spektroskopiker Johannes Rydberg gefunden. Mit der von ihm aufgestellten Formel lassen sich die Frequenzen aller Emissionslinien des Wasserstoffs berechnen:

, n=ganze Zahl, n₂ > n₁
(Für die Balmer-Serie ist n₂=2)
Die Balmer-Serie und die Rydberg-Formel erwiesen sich als wichtige Grundlagen für die Ausarbeitung des Bohrschen Atommodells.

Aufgabe 2.7.1.3:
Lösung Bohr fand einen Ausdruck, der die Rydberg-Konstante oder -Frequenz durch Naturkonstanten ausdrückt:

R_H=(m_e×e⁴ / 8x³ × e₀²)

mit: e ₀= Dielektrizitätskonstante im Vakuum, 8.85 × 10^-12 C²/(J m)
e=Elementarladung, 1.602×10^-19 C
m_e=Masse des Elektrons, 9.11×10^-31 kg
Welche Einheit hat der Faktor x? Um welche Naturkonstante handelt es sich?

Aufgabe 2.7.1.4:
Lösung Die Rydberg-Konstante läßt sich auch durch folgenden Ausdruck darstellen:

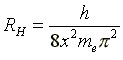Welchen Wert und welche Einheit hat der Faktor x. Um welchen Wert handelt es sich?

Aufgabe 2.7.1.5:
Lösung Welche Wellenlänge hat ein Photon, daß beim Übergang zwischen den beiden Zuständen n₁=2 und n₂=4 emittiert wird?

zurück